Set

What is Set?

The collection of well-defined objects is called a Set. The set is generally represented by the capital letters of English letters. The objects in the collection are called members of that set. 

Set Operations

There are four primary set operations in mathematics:

1. Union (\(\cup\)): Combines all elements from both sets, removing duplicates.

2. Intersection (\(\cap\)): Finds common elements that exist in both sets.

3. Difference (\(-\)): Finds elements that are in one set but not in the other.

4. Complement (\(A'\) or \(A^c\) or \(\bar{A}\)): Contains all elements not in the specified set, assuming a universal set.

Here are definitions and examples for each of the four primary set operations:

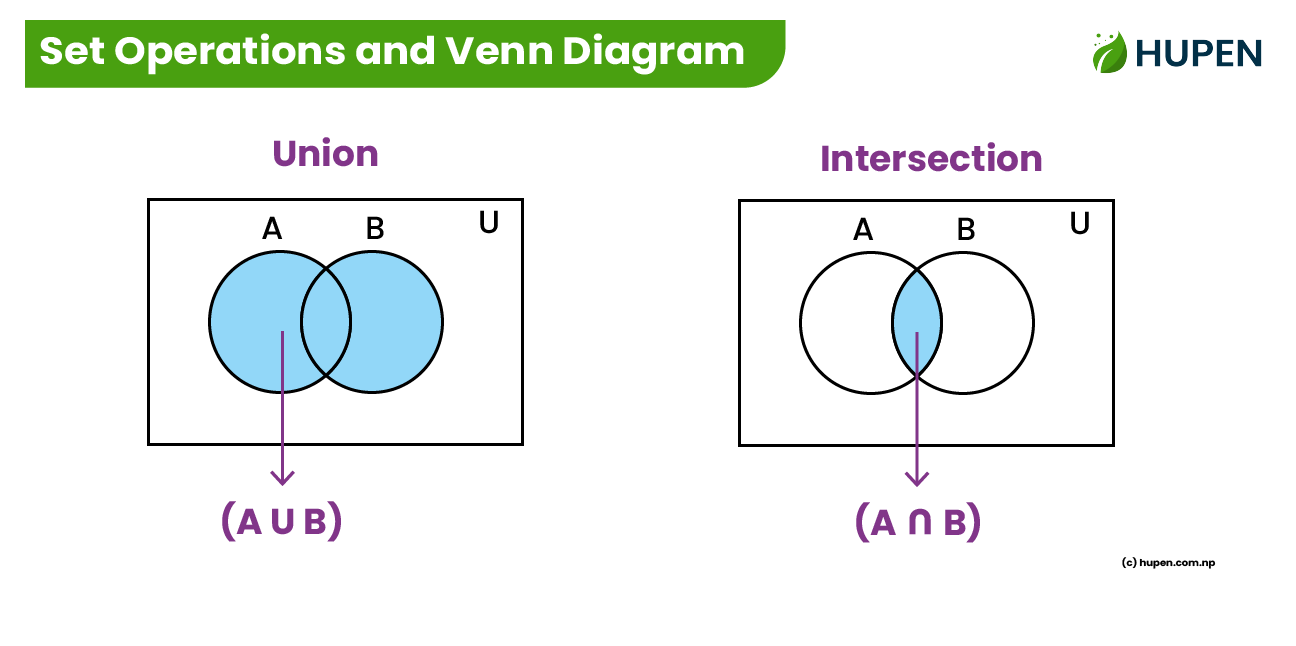
1. Union (\(\cup\))

Definition: The union of two sets \(A\) and \(B\), denoted by \((A \cup B)\), is the set of elements that are in \(A\), in \(B\), or in both.

Example:

Let \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \). 

Then, \( A \cup B = \{1, 2, 3, 4, 5\} \).

2. Intersection (\(\cap\))

Definition: The intersection of two sets \(A\) and \(B\), denoted by \((A \cap B)\), is the set of elements that are in both \(A\) and \(B\).

Example:

Let \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \). 

Then, \( A \cap B = \{3\} \).

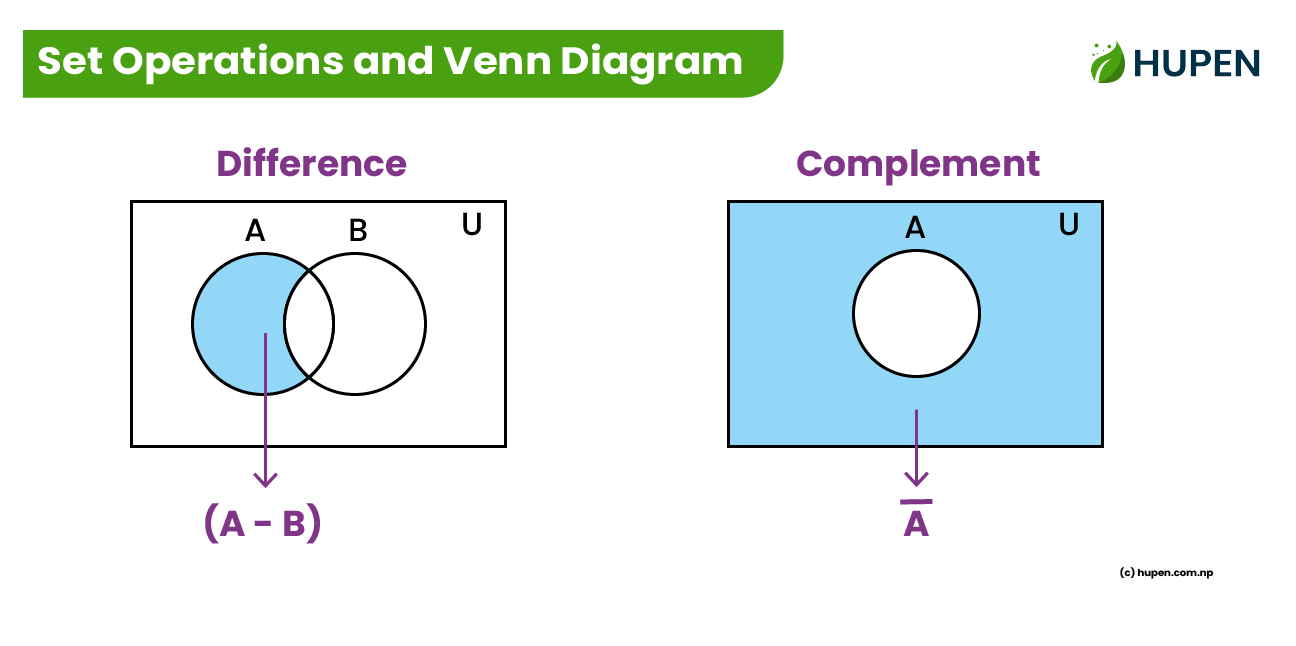
3. Difference (\(-\))

Definition: The difference between two sets \(A\) and \(B\), denoted by \((A - B)\), is the set of elements that are in \(A\) but not in \(B\).

Example: 

Let \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \). 

Then, \( A - B = \{1, 2\} \), and \( B - A = \{4, 5\} \).

4. Complement (\(A'\) or \(A^c\) or \(\bar{A}\))

Definition: The complement of a set \(A\), denoted by \(A'\) or \(A^c\) or \(\bar{A}\), is the set of elements that are in the universal set \(U\) but not in \(A\).

Example: 

If the universal set \( U = \{1, 2, 3, 4, 5\} \) and \( A = \{1, 2, 3\} \), 

then the complement of \(A\) or \( \bar{A} = \{4, 5\} \).

Venn Diagram of Set Operations