Cylinder and Sphere
Class 9: Mathematics
Cylinder, Formulas for a Cylinder, Sphere, Formulas for a Sphere, Semi-Sphere, Formulas for a hemisphere, Example Questions
Cylinder
A cylinder is a three-dimensional shape with two parallel circular bases and a curved surface connecting them. The line segment joining the centers of the two circular bases is called the axis of the cylinder. If the axis is perpendicular to the bases, the cylinder is called a right circular cylinder; otherwise, it is an oblique cylinder.
Formulas for a Cylinder
Here are the main formulae related to a cylinder:
1. Volume of a Cylinder
The volume of a cylinder measures the amount of space it occupies.
\(\text{Volume (V)} = \pi r^2 h\)
where:
- \( r \) = radius of the base
- \( h \) = height (distance between the two bases)
2. Curved Surface Area (CSA) of a Cylinder
The curved surface area (or lateral surface area) is the area of just the curved side of the cylinder.
\(\text{Curved Surface Area (CSA)} = 2 \pi r h\)
where:
- \( r \) = radius of the base
- \( h \) = height of the cylinder
3. Total Surface Area (TSA) of a Cylinder
The total surface area is the sum of the curved surface area and the areas of the two circular bases.
\(\text{Total Surface Area (TSA)} = 2 \pi r (r + h)\)
where:
- \( r \) = radius of the base
- \( h \) = height of the cylinder
Sphere
A sphere is a perfectly round, three-dimensional object in which every point on its surface is equidistant from its center. It has no edges or vertices and is a type of solid in geometry.
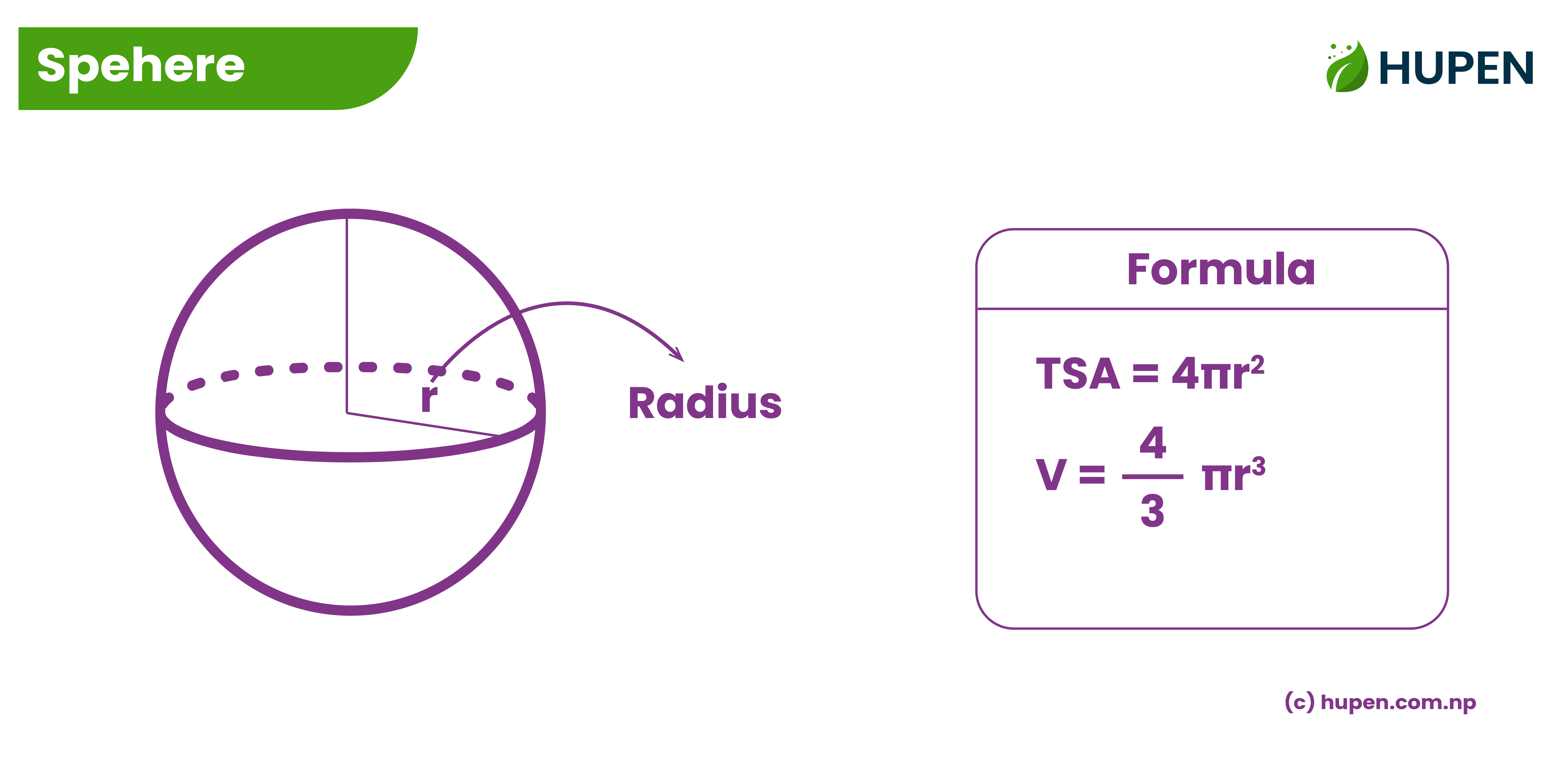
Formulas for a Sphere
1. Surface Area of a Sphere
The surface area of a sphere is the total area covered by its outer surface. It is measured in square units and represents the area of the curved, continuous surface of the sphere.
\(\text{Surface Area} = 4 \pi r^2\)
where \( r \) is the radius of the sphere.
2. Volume (V) of a Sphere
The volume of a sphere is the amount of space enclosed within the sphere. It is measured in cubic units and represents the capacity or the three-dimensional space occupied by the sphere.
\(\text{Volume} = \frac{4}{3} \pi r^3\)
where \( r \) is the radius of the sphere.
Hemisphere (Semi-Sphere)
A hemisphere (or semi-sphere) is half of a sphere, divided by a plane passing through its center. It has a curved surface and a flat circular base.
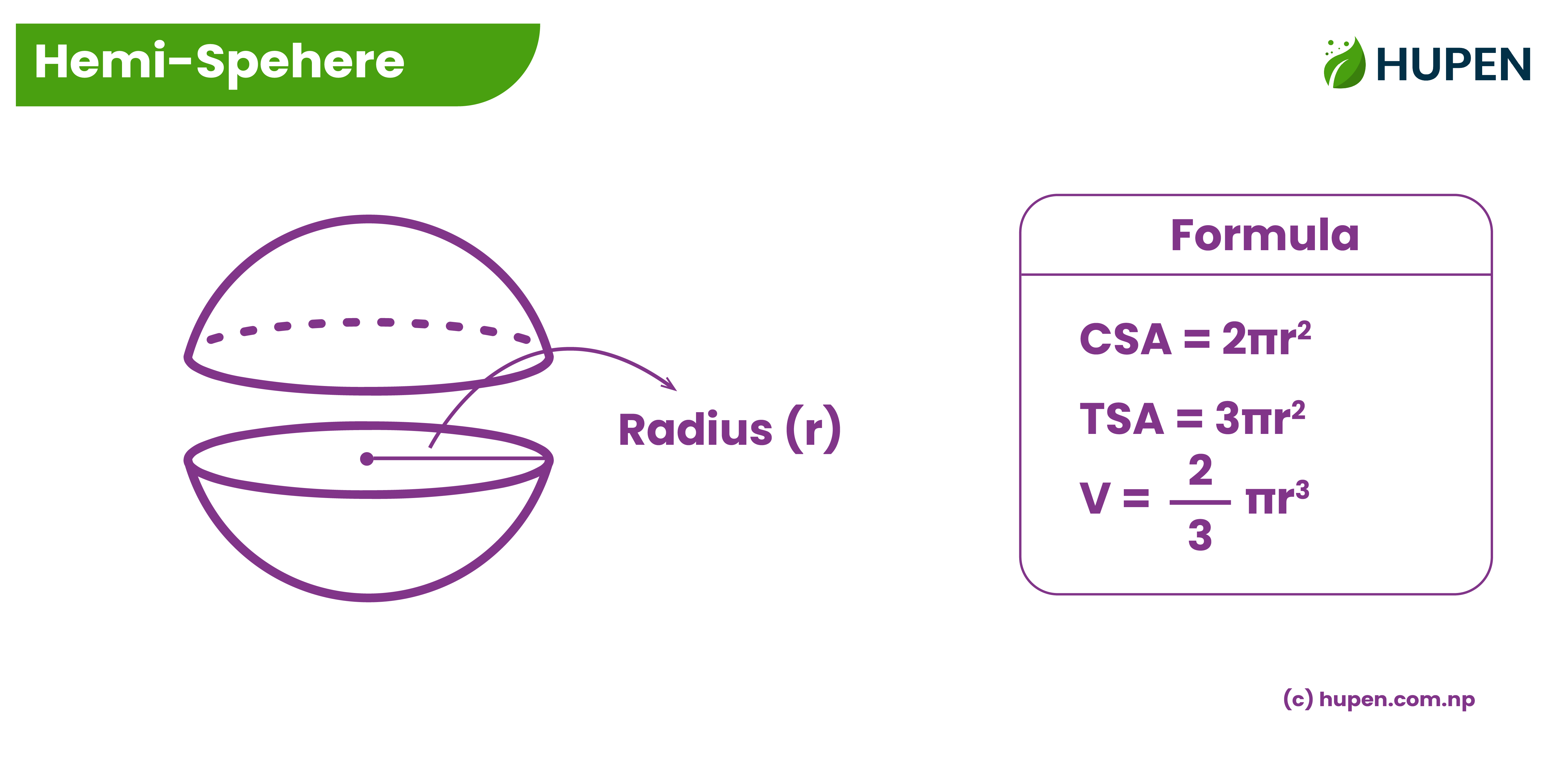
Formulas for a Hemisphere
1. Curved Surface Area (CSA): only the curved part, without the flat base
The curved surface area of a hemisphere refers only to the curved, dome-shaped portion, excluding the flat circular base. It is the outer area of the semi-spherical surface.
\(\text{Curved Surface Area} = 2 \pi r^2\)
where \( r \) is the radius of the hemisphere.
2. Total Surface Area (TSA): curved surface + flat circular base
The total surface area of a hemisphere includes both the curved surface and the flat circular base. It is the entire area covering both parts of the hemisphere.
\(\text{Total Surface Area} = 3 \pi r^2\)
where \( r \) is the radius of the hemisphere.
3. Volume of a Hemisphere:
The volume of a hemisphere is the amount of space enclosed within the semi-spherical shape. It represents half the volume of a complete sphere, as a hemisphere is exactly half of a sphere.
\(\text{Volume} = \frac{2}{3} \pi r^3\)
where \( r \) is the radius of the hemisphere.
