Introduction

In mathematics, the concept of a set is foundational, forming the basis of set theory and its operations. Sets allow us to group elements—numbers, objects, or even concepts—and define relationships between different groups through operations. This post will guide you through the basics of sets, followed by an in-depth look at set operations with examples and practice questions to solidify your understanding.

What is a Set?

A set is simply a collection of distinct elements or objects. Sets are usually represented by curly brackets { }, with each element separated by a comma. For example:

- Set of Colors: \( C = \{\text{red, blue, green}\} \)

- Set of Numbers: \( N = \{1, 2, 3, 4\} \)

Sets are typically named with capital letters like \( A \), \( B \), \( C \), etc. The items inside a set are called elements or members.

Types of Set Operations

Sets can interact with each other in different ways. These interactions, called set operations, allow us to combine, compare, and analyze relationships between sets. Here are the main set operations:

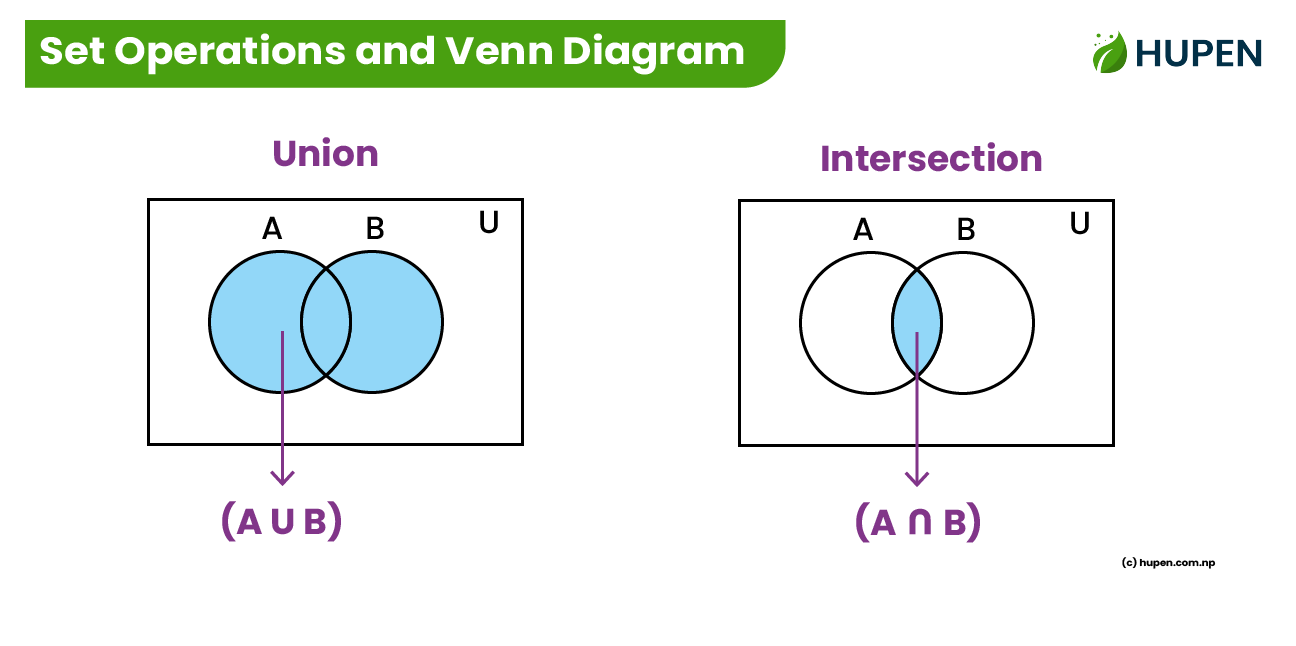
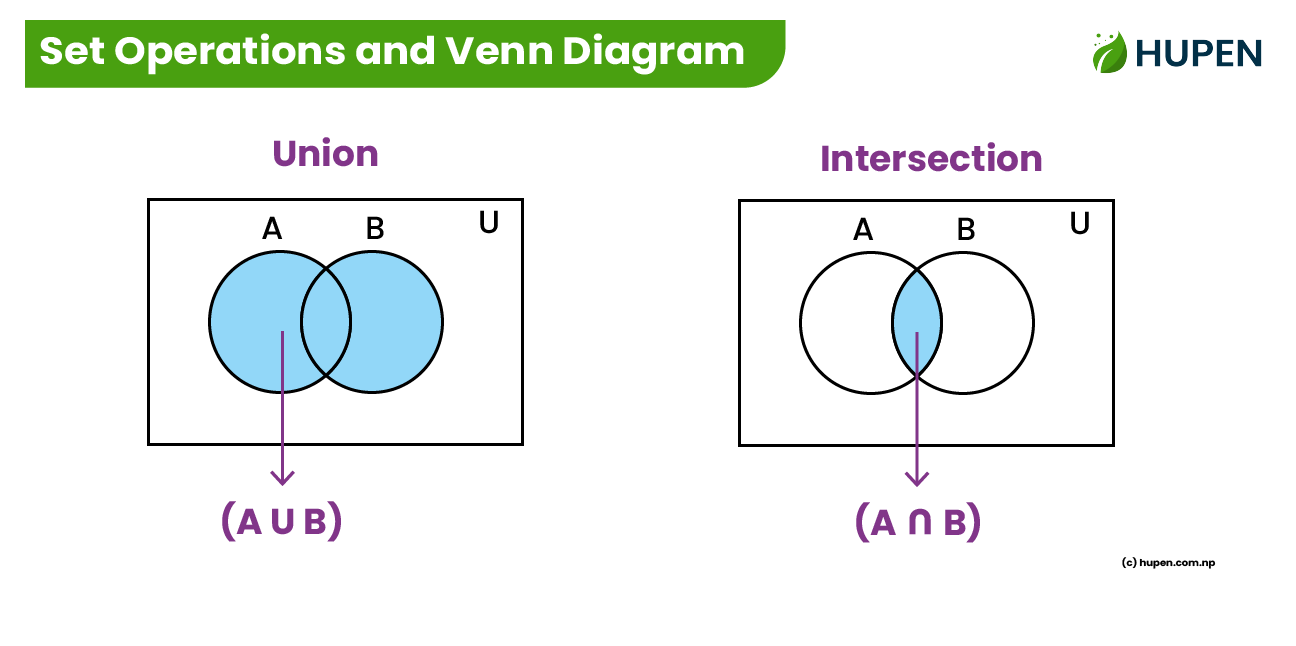
1. Union ( \( A \cup B \) )

The union of two sets \( A \) and \( B \) includes all elements that are in either \( A \), \( B \), or both.

- Definition: \( A \cup B = \{ x : x \in A \text{ or } x \in B \} \)

- Example: 

  If \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \), then \( A \cup B = \{1, 2, 3, 4, 5\} \).

2. Intersection ( \( A \cap B \) )

The intersection of two sets \( A \) and \( B \) includes only the elements that are in both \( A \) and \( B \).

- Definition: \( A \cap B = \{ x : x \in A \text{ and } x \in B \} \)

- Example: 

  If \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \), then \( A \cap B = \{3\} \).

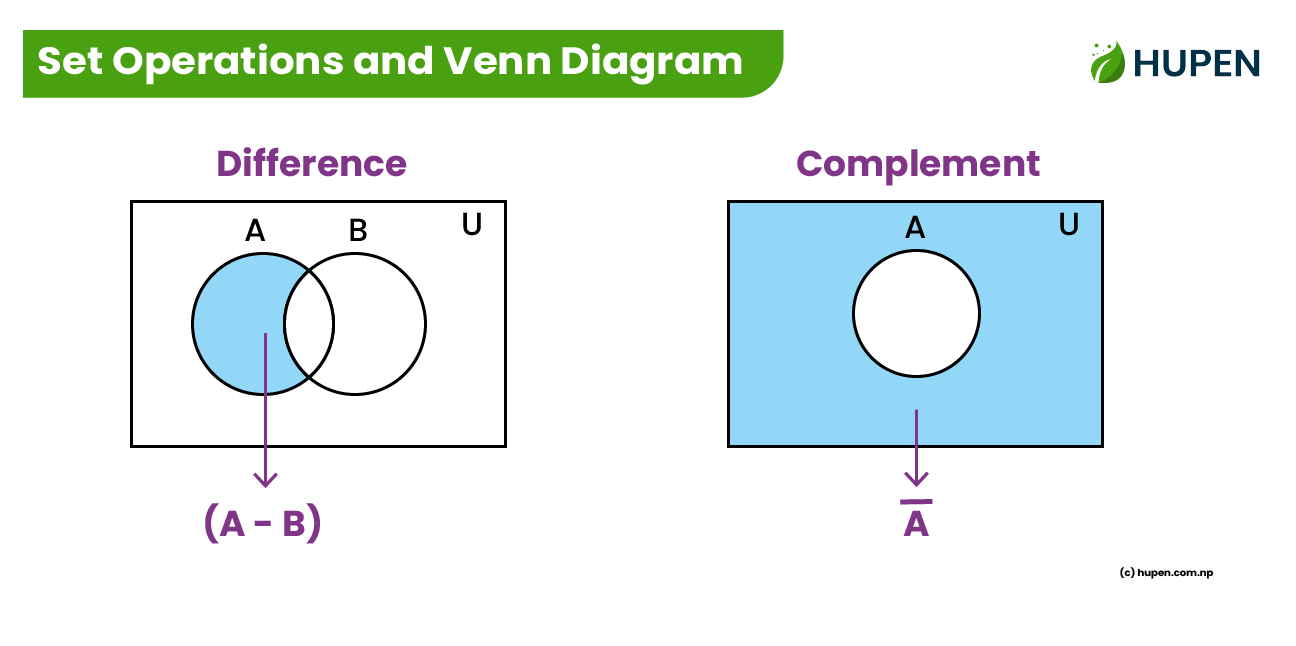
3. Difference ( \( A - B \) or \( A \setminus B \) )

The difference of two sets \( A \) and \( B \) contains elements that are in \( A \) but not in \( B \).

- Definition: \( A - B = \{ x : x \in A \text{ and } x \notin B \} \)

- Example: 

  If \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \), then \( A - B = \{1, 2\} \).

4. Symmetric Difference ( \( A \Delta B \) )

The symmetric difference of two sets \( A \) and \( B \) includes elements that are in either \( A \) or \( B \), but not in both.

- Definition: \( A \Delta B = \{ x : x \in A \text{ or } x \in B, \text{ but } x \notin A \cap B \} \)

- Example: 

  With \( A = \{1, 2, 3\} \) and \( B = \{3, 4, 5\} \), then \( A \Delta B = \{1, 2, 4, 5\} \).

5. Complement ( \( A'  or A^c or \bar{A}\) )

The complement of a set \( A \) (with respect to a universal set \( U \)) contains all elements in \( U \) that are not in \( A \).

- Definition: \( A' = \{ x : x \in U \text{ and } x \notin A \} \)

- Example: 

  If \( U = \{1, 2, 3, 4, 5, 6\} \) and \( A = \{1, 2, 3\} \), then \( \bar{A} = \{4, 5, 6\} \).

Venn Diagrams for Set operations:

Practice Questions

Try solving these practice questions to reinforce your understanding:

Question 1: Union of Sets

If \( A = \{2, 4, 6, 8\} \) and \( B = \{4, 5, 6, 9\} \), find \( A \cup B \).

Answer: 

\( A \cup B = \{2, 4, 5, 6, 8, 9\} \).

Question 2: Intersection of Sets 

If \( A = \{1, 2, 3, 4\} \) and \( B = \{3, 4, 5, 6\} \), find \( A \cap B \).

Answer: 

\( A \cap B = \{3, 4\} \).

Question 3: Difference of Sets 

If \( A = \{a, b, c, d\} \) and \( B = \{b, d, e\} \), find \( A - B \).

Answer: 

\( A - B = \{a, c\} \).

Question 4: Symmetric Difference 

Given \( A = \{10, 20, 30\} \) and \( B = \{20, 40, 50\} \), find \( A \Delta B \).

Answer: 

\( A \Delta B = \{10, 30, 40, 50\} \).

Question 5: Complement of a Set

Assume \( U = \{1, 2, 3, 4, 5, 6, 7, 8\} \) and \( A = \{2, 4, 6, 8\} \). Find \( A' \).

Answer: 

\(A^c = \{1, 3, 5, 7\} \).

Conclusion

Understanding sets and set operations is fundamental in mathematics. These basic concepts form the foundation of many fields, such as data science, probability, and computer science. With these definitions, examples, and practice questions, you’re now well-equipped to explore more complex mathematical topics involving sets.