Introduction

Linear motion is a fundamental concept in physics, describing the movement of an object along a straight path with constant acceleration. In this post, we'll dive into the three equations of linear motion, which relate to the object's velocity, displacement, time, and acceleration. Understanding these equations will give you a deeper grasp of kinematics, the study of motion.

What is Linear Motion?

Linear motion refers to movement in a straight line. If the object is moving under constant acceleration, we can use three equations to describe its motion. These equations are essential tools for solving problems related to velocity, displacement, and time in physics.

Before we derive these equations, let's define the key terms:

- u: Initial velocity (the velocity at the start of the motion)

- v: Final velocity (the velocity after time \( t \))

- a: Constant acceleration

- t: Time taken

- s: Displacement (the distance covered during the motion)

First Equation of Motion:

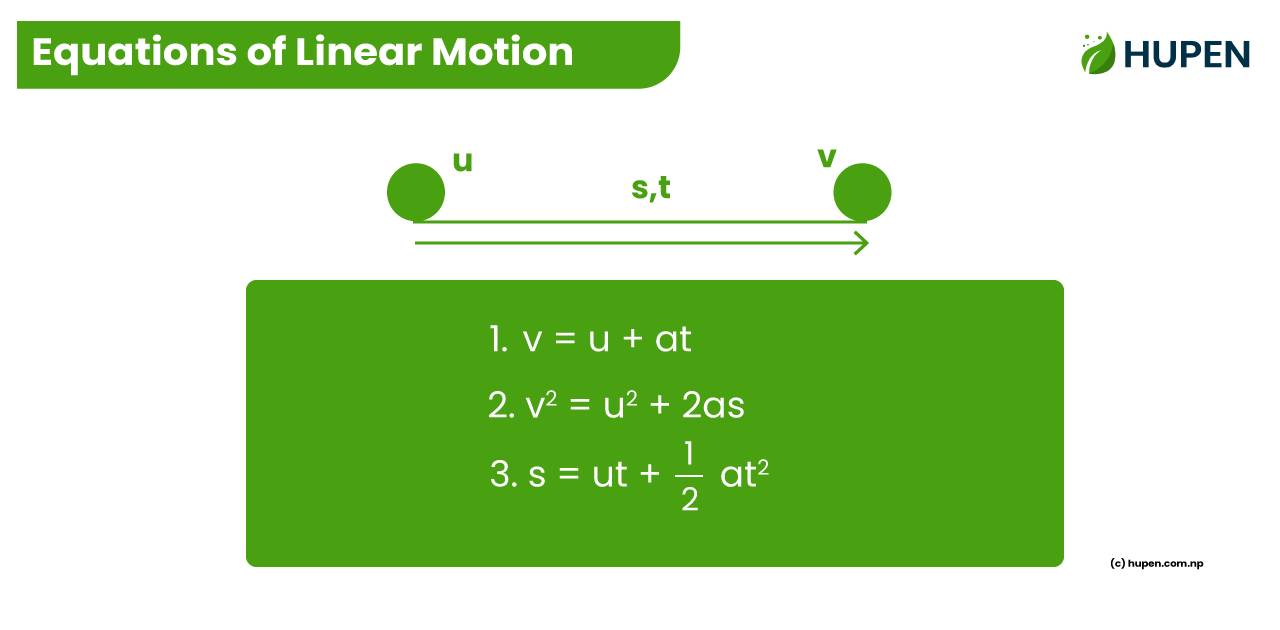
The first equation is: \(v = u + at\)

This equation relates an object’s final velocity to its initial velocity, acceleration, and time. Here’s how we derive it:

Derivation:

• Acceleration is defined as the rate of change of velocity. Mathematically:

\(a = \frac{v - u}{t}\)

• Rearranging this equation to solve for the final velocity \( v \):

\(\therefore v = u + at\)

This is the first equation of motion, which gives the object's velocity after time \( t \) when it is moving with constant acceleration.

Second Equation of Motion:

The Second Equation is: \(s = ut + \frac{1}{2}at^2\)

This equation describes the displacement of an object after a certain time under constant acceleration.

Derivation:

• The displacement \( s \) is the distance covered by an object. For motion with constant acceleration, we calculate displacement using the average velocity:

\(\text{Average velocity} = \frac{u + v}{2}\)

• Displacement \( s \) is given by:

\(s = \text{Average velocity} \times t = \left( \frac{u + v}{2} \right) t\)

Substituting \( v = u + at \) from the first equation into this equation:

\(s = \left( \frac{u + (u + at)}{2} \right) t\)

Simplifying:

\(\text{or,} s = \left( \frac{2u + at}{2} \right) t \)

\(\therefore s = ut + \frac{1}{2}at^2\)

This is the second equation of motion, which gives the object’s displacement after time \( t \).

Third Equation of Motion:

The third equation is: \(v^2 = u^2 + 2as\)

The third equation relates the final velocity to the initial velocity, acceleration, and displacement.

Derivation:

• Starting with the first equation:

\(v = u + at\)

Solve for time \( t \):

\(\text{or, } t = \frac{v - u}{a}\)

• Substitute this value of \( t \) into the second equation , we get,

\(\text{or, } s = ut + \frac{1}{2}at^2\)

Now, we substitute \( t = \frac{v - u}{a} \) into this equation:

\(\text{or,} s = u \frac{v - u}{a} + \frac{1}{2} a \frac{(v - u)^2}{a^2}\)

\(\text{or,} s = \frac{u(v - u)}{a} + \frac{(v - u)^2}{2a}\)

• Multiply both sides by \( 2a \) to eliminate the denominators:

\(\text{or,} 2as = 2u(v - u) + (v - u)^2\)

\(\text{or,} 2as = v^2 - u^2\)

\(\therefore v^2 = u^2 + 2as \)

This is the third equation of motion, which relates the final velocity \( v \) to the initial velocity \( u \), displacement \( s \), and acceleration \( a \).

Conclusion

The three equations of linear motion are critical for understanding and solving problems in physics related to objects moving with constant acceleration:

1. First equation: \( v = u + at \)

2. Second equation: \( s = ut + \frac{1}{2}at^2 \)

3. Third equation: \( v^2 = u^2 + 2as \)

These equations help describe how objects move in a straight line under uniform acceleration, and they’re foundational in both theoretical and practical applications of physics.